前回の記事

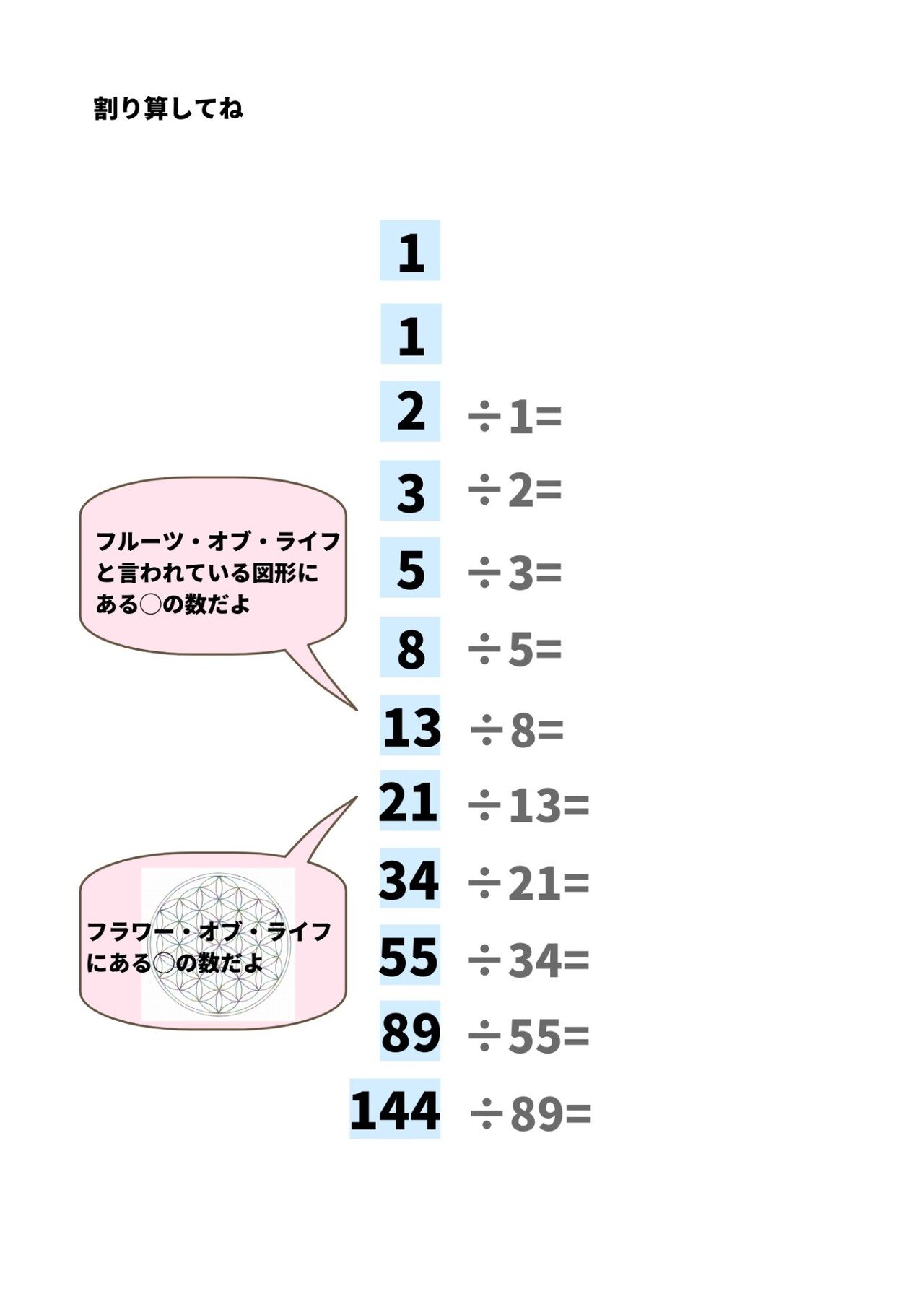
まずは下を見て電卓を用意して計算してみてくださいね。 

だんだんとこのφ（ファイ）に近づいて来ているのがわかりますか？

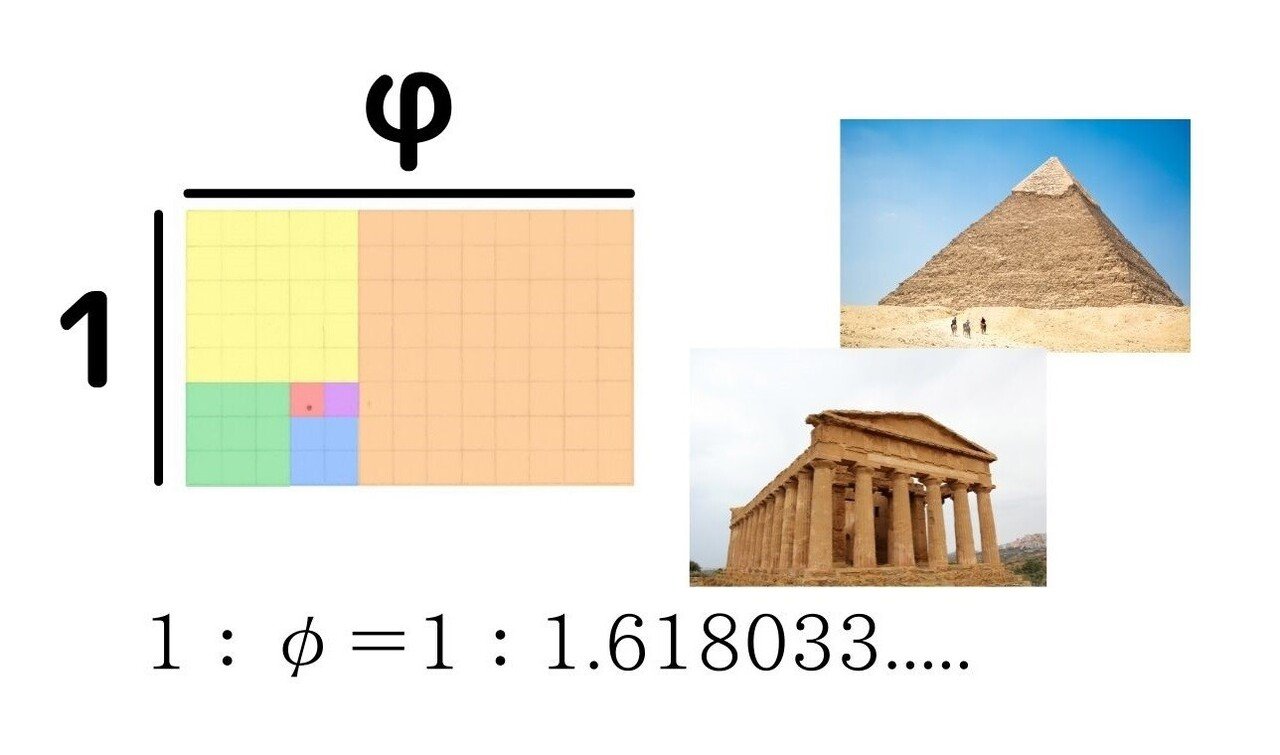
この1:φの比率を黄金比といいます。
ピラミッドやパルテノン神殿等の歴史的建造物、そして私たちのからだの中にもこのバランスがあると言われています。

でも、このフィボナッチの割り算は、どんなに頑張ってもφにはなれません。この数字をCGで表すのなら、

φの回りをくるくる回っているんでしょうね。 

このフィボナッチとファイを人生観等に当てはめるととても生きやすい気持ちになります。（長くなりますのでその話は別の機会に）

フィボナッチと言えばひまわり。近所のひまわり畑で撮った写真です。この種のカーブがフィボナッチ（ここの向日葵は小さいのでちょっとわかりにくいですね。）

おっと関係のない写真が❗️可愛いのでそのまま載せます

種になるとよくわかりますね。

大きなひまわりの場合、カーブが右と左にわかれます。そして、種の数が不思議なことにフィボナッチ数列と当てはまります。

このカーブ、そして松ぼっくりもフィボナッチ。こちらも数がフィボナッチ数列と当てはまるんですよ。

(^^)/ちょっとへそまがりの方のために補足(笑)個体差があるので全部が当てはまるとは言いきれませんが、平均値とお取りくださいね）

そして余談ですが松ぼっくりは松果体。松果体の事は神聖幾何学模様アートのホルスの目でちょっとお話ししています。

松ぼっくりが落ちているのを見て「あっ！松果体」と思ったらあなたもかなりの神聖幾何学マニアです（笑）

下の画像はこのカーブを表していると言われています。

オウムガイは有名ですね。（数学関係の記事で真実ではないというのを読みましたが、一般的には言われていますので掲載しました。）

台風、ハリケーンも渦巻き、渦巻き銀河もこのカーブに似ていますね😃

写楽の絵もあります。モナリザもあてはまります。

美しいと言われる物を描いたり作った昔の人の作品に、このカーブが当てはまるのが不思議ですね

カーブを描いてみますか？動画ではゴールデンスパイラルと言っていますが、同じものです。  

ゴールデンスパイラルとは神聖幾何学模様アート、絵の方でお伝えしています。興味のある方はこちらのマガジンも是非

動画にも出てくるこちらの糸かけは１５cmの正方形の板で作っています。
もう少し複雑なのはシリーズ④のフィボナッチの行進を見てくださいね

釘を打つ位置を記したピンシートの作り方が動画でも触れています。動画を見て自分で作ってみても良いですね😃

フィボナッチシリーズ④のフィボナッチの行進で①～④までの資料を有料ですがダウンロードできます。そちらは下の写真のように一つ大きなタイプのフィボナッチになります。

糸のかけ方を説明しますね😃

スタート位置は１+１の真ん中です。

クロスになるように糸をかけます。刺繍糸を使っています。

最初の１が出来ました。

色をかえて、もう一つの１を同じように糸をかけます。

次に写真の位置に糸を結びます。（動画で説明しているコンパスの針を刺す場所です。）

写真のように、1/4円ずつ色をかえながらかけていきます。

スタート位置はコンパスの針を刺す場所です。

最後に、外側のカーブに糸をかけます。写真では藤色を使っています。出来上がりの15cmの板で作ったサンプルは金の糸を絡ませながら作りました。

ちょっとアレンジ。30cmです。 

糸を渡している線に等間隔で釘を打ちました。まるでナウシカに出てくるオームのようになりました(笑)

こちらは神聖幾何学模様アート、絵でゴールデンスパイラルとしてお伝えしていものです

note掲載「フィボナッチ」シリーズのワークシートは↓