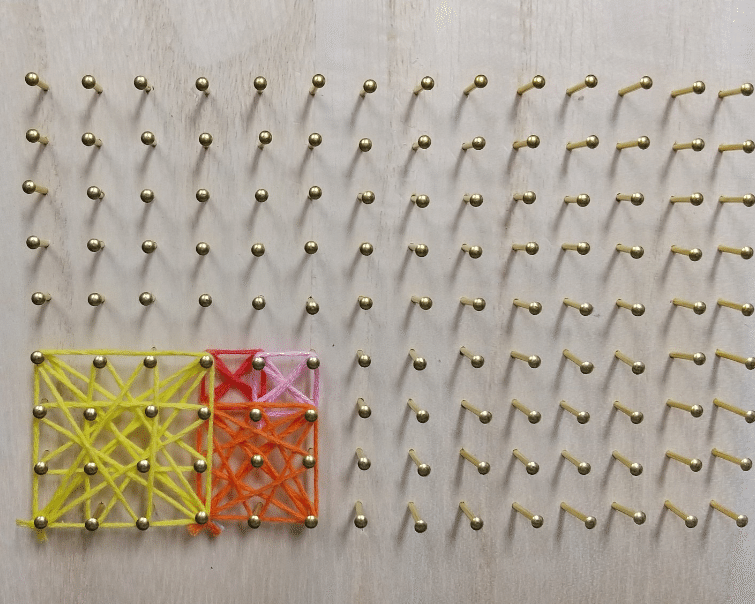フィボナッチ数列（フィボナッチ数列）は、0と1で始まり、それ以降の数が直前の2つの数の和として定義される数列です。 具体的には、0、1、1、2、3、5、 8、13、21、34、55、...と続いていきます。

数学的には、フィボナッチ数列は再び戻ってくる関係式で表されます。n番目のフィボナッチ数をFnとすると、以下の関係が成り立ちます。

Fn = Fn-1 + Fn-2

ただし、F0 = 0、F1 = 1となります。

フィボナッチ数列は、自然界や科学、芸術など幅広い分野で見られます。例えば、植物の花弁の数や巻き貝の殻の螺旋など、自然界の構造に現れることが知られています。の応用、アルゴリズムの最適化などでも利用されます。

フィボナッチ数列の特徴的な性質として、数列の各項を前の項で割ると、近似的に黄金比（1.61803）に収束するという性質があります。この性質は、美しい観点やデザインにおいても用いられるられることがあります。

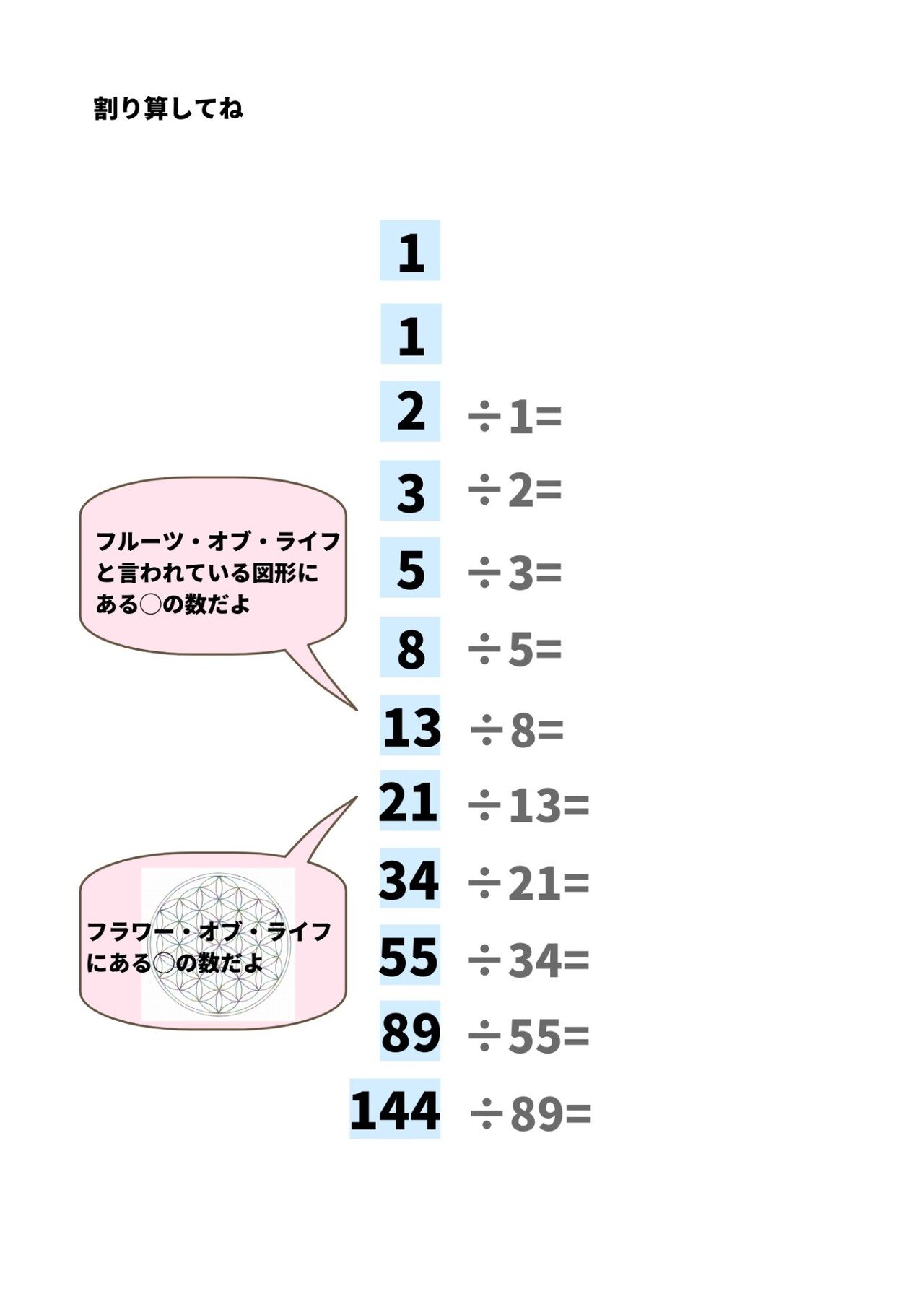
神聖幾何学的にこのフィボナッチ数列の並びを見てみると、その中にはフラワーオブライフの21、フルーツオブライフの13が含まれていることがわかります。

それではその黄金比とは何でしょうか

黄金比（Golden Ratio）とスパイラル（Golden Spiral）は、数学と美学の分野で広く知られている概念です。

黄金比は、二つの異なる長さの線分に関して、長い方の線分全体を短い方の線分さの長さに対する比が、短い方の線分を長い方の線分の長さに対する比と一般的には、この比をギリシャ文字のフィ（Φ）で表し、およそ1.6180339887という近似値で表されます。 黄金比は、古代ギリシャの芸術や建築において頻繁に様々な自然物や芸術作品にも見られることがあります。

ゴールデンものです。ゴールデンスパイラルは、黄金比に基づいて描かれた渦巻状の曲線です。 スパイラルは、中心から外側に向かって一定の比率で螺旋状に進行していく特徴を持ちます。同様に、多くの植物の成長のパターンや、巻貝の殻の形状などがスパイラルに近い形として知られていて神聖幾何学としてもとても興味深いものです。

虹色のグラデーションで作ったフィボナッチの糸かけ。
糸かけにしないで、線を引いても綺麗ですね（＾＾）

フィボナッチの行進は２０ｃｍ×６０ｃｍの板を使っています。
ホームセンターなどで売っている焼き色のついた板で作りました。

大きな形の場合、３０ｃｍの正方形だと板が大きすぎて、２０ｃｍだと入りません。真ん中の大きさでしたら１５ｃｍの板でも大丈夫です。
作りたい板があるようでしたら、型紙をレイアウトしてみてくださいね。

最初は紫からかけていきます（＾＾）

↑ここがスタート。ほどけないように結んでね。

糸はスタートは左からでて、右に入る来るっとまわってスタートの釘に右から入ります。そうすると、次も左から出られるでしょ（＾＾）

一つ終わったら糸をカーブにかけながら次のスタート地点まで。

それを最後までするとこんな感じ。
糸はスタートに戻って結んでから切ります。

スタートの釘の位置を一つずつ変えながら6色の糸を掛けていきます

テキストは↓よりお求めいただけます。

前回の記事のつづき

太陽の恵みを平等に浴びて成長している樹

どうして平等なのか、考えたことありますか？

実は黄金角を作りながら枝をだしているからなんです。

黄金角とは円周を黄金比で分割した時の短い方と中心を繋いで出来る角度です。

137.507764、、、、割りきれません

そして、重なりません。（いずれは重なるかもしれないですが、、、）だから、太陽の光が平等に届くわけです。

どうしてもこの黄金角をこの目で見たくて、自分で分割出来る近似値で作ったのがこの黄金角の糸かけです。

見ているだけで癒される不思議な形ですよ😃

作り方は簡単。黄金角のシートに描いてある数字の番号順に糸をかけていくだけ。

※シートのPDFは記事の一番下にあります（有料）

真ん中スタート、１に糸をかけて、真ん中に戻って、次に２に糸をかける

そんな感じで順番にかけていきます。

画像はフィボナッチを一つ入れるので30ｃｍで作っています。20ｃｍの板で作れます。  

右下の赤は15ｃｍの板で作って、枝を多く出したものです。

興味のある方は↓に進んでくださいね。

前回の記事

まずは下を見て電卓を用意して計算してみてくださいね。 

だんだんとこのφ（ファイ）に近づいて来ているのがわかりますか？

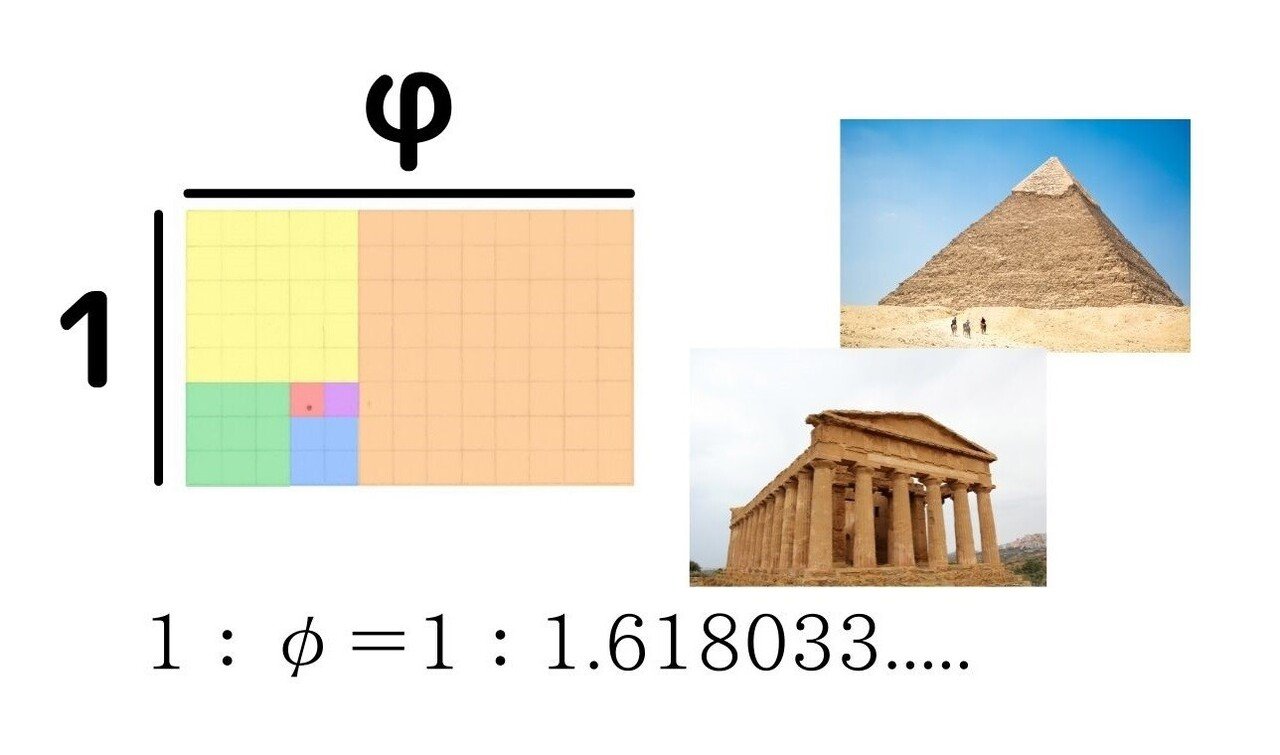
この1:φの比率を黄金比といいます。
ピラミッドやパルテノン神殿等の歴史的建造物、そして私たちのからだの中にもこのバランスがあると言われています。

でも、このフィボナッチの割り算は、どんなに頑張ってもφにはなれません。この数字をCGで表すのなら、

φの回りをくるくる回っているんでしょうね。 

このフィボナッチとファイを人生観等に当てはめるととても生きやすい気持ちになります。（長くなりますのでその話は別の機会に）

フィボナッチと言えばひまわり。近所のひまわり畑で撮った写真です。この種のカーブがフィボナッチ（ここの向日葵は小さいのでちょっとわかりにくいですね。）

おっと関係のない写真が❗️可愛いのでそのまま載せます

種になるとよくわかりますね。

大きなひまわりの場合、カーブが右と左にわかれます。そして、種の数が不思議なことにフィボナッチ数列と当てはまります。

このカーブ、そして松ぼっくりもフィボナッチ。こちらも数がフィボナッチ数列と当てはまるんですよ。

(^^)/ちょっとへそまがりの方のために補足(笑)個体差があるので全部が当てはまるとは言いきれませんが、平均値とお取りくださいね）

そして余談ですが松ぼっくりは松果体。松果体の事は神聖幾何学模様アートのホルスの目でちょっとお話ししています。

松ぼっくりが落ちているのを見て「あっ！松果体」と思ったらあなたもかなりの神聖幾何学マニアです（笑）

下の画像はこのカーブを表していると言われています。

オウムガイは有名ですね。（数学関係の記事で真実ではないというのを読みましたが、一般的には言われていますので掲載しました。）

台風、ハリケーンも渦巻き、渦巻き銀河もこのカーブに似ていますね😃

写楽の絵もあります。モナリザもあてはまります。

美しいと言われる物を描いたり作った昔の人の作品に、このカーブが当てはまるのが不思議ですね

カーブを描いてみますか？動画ではゴールデンスパイラルと言っていますが、同じものです。  

ゴールデンスパイラルとは神聖幾何学模様アート、絵の方でお伝えしています。興味のある方はこちらのマガジンも是非

動画にも出てくるこちらの糸かけは１５cmの正方形の板で作っています。
もう少し複雑なのはシリーズ④のフィボナッチの行進を見てくださいね

釘を打つ位置を記したピンシートの作り方が動画でも触れています。動画を見て自分で作ってみても良いですね😃

フィボナッチシリーズ④のフィボナッチの行進で①～④までの資料を有料ですがダウンロードできます。そちらは下の写真のように一つ大きなタイプのフィボナッチになります。

糸のかけ方を説明しますね😃

スタート位置は１+１の真ん中です。

クロスになるように糸をかけます。刺繍糸を使っています。

最初の１が出来ました。

色をかえて、もう一つの１を同じように糸をかけます。

次に写真の位置に糸を結びます。（動画で説明しているコンパスの針を刺す場所です。）

写真のように、1/4円ずつ色をかえながらかけていきます。

スタート位置はコンパスの針を刺す場所です。

最後に、外側のカーブに糸をかけます。写真では藤色を使っています。出来上がりの15cmの板で作ったサンプルは金の糸を絡ませながら作りました。

ちょっとアレンジ。30cmです。 

糸を渡している線に等間隔で釘を打ちました。まるでナウシカに出てくるオームのようになりました(笑)

こちらは神聖幾何学模様アート、絵でゴールデンスパイラルとしてお伝えしていものです

note掲載「フィボナッチ」シリーズのワークシートは↓

 フィボナッチのマス目を利用して、色を入れていったこの黄金長方形の絵を
「フィボナッチタイル」と呼んでいます。

その時その時で色の雰囲気や配置が違うのでとてもきれい
みんなそれぞれ違うものが出来て、雰囲気も違うのは面白いです。

もしかしたら、宇宙は私たちをコードで認識していたら
こんな感じの模様で届いているかもしれないですね。

フィボナッチ数列についてお話ししますね。まずは下の足し算をしてみてください。

１，１，３，５，８，１３，２１，３４，５５，８９，１４４、、、、、

足し続けるから、永遠に増えていく数列です。

フィボナッチさん、ある日ウサギが増えていくのを見てあれ？となり
この足し算を見つけたそうです。ウサギさんて多産なんです（＾＾）

１はウサギの雄、もう一つの1はウサギの雌、2で一緒になって
そしたら３で子供が生まれたよって感じですね。

でね。ここで出た数字の中に実は神聖幾何学的に大切な数があるんです。
（それは別の項目で説明しますね）

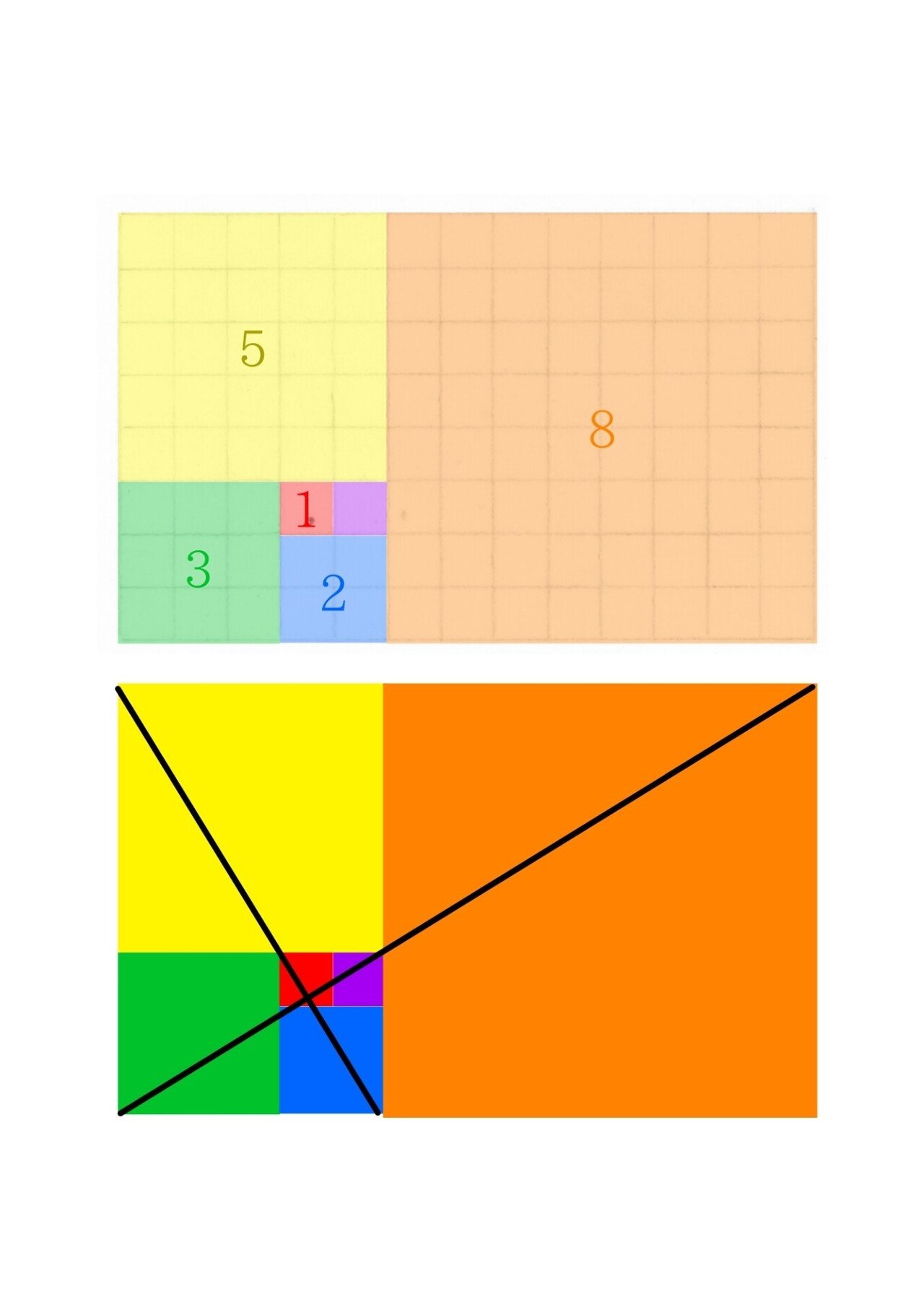
では、下のマス目の図を見てくださいね。
上の足し算で出た数を1辺にして正方形になるように色を入れています。
（ここでφというものが出てきますが、それも別の項目でお話しします）

私がこれを習ったのは服飾専門学校のデザインの時間です。
この分割比率で切り替えをつけるとバランスがいいとか

シャネルがミニスカートを発表した時の、ウエストや切り替えのバランスがこの比率（に近い）だったから美しいものが出来たって習った気がします30年以上前の話（笑）日本の着物が美しいのも帯との比率がこれだからって聞いたこともあります。

上の×はなんだと思いますか？？
フィボナッチ数列でどんどん長方形が大きくなっても、必ず通る位置です。
「神の目」ともいわれています。

（このフィボナッチシリーズでは入れていませんが、神聖幾何学の絵にはゴールデンスパイラルというものがあります。これはスタートがフィボナッチの１か×の交点かでの違いです。）

フィボナッチタイルではその神の目の位置を点でいれています。

こちらは糸かけ。出来てくる正方形を一つの塊として糸をかけました。フィボナッチタイルのように色を変えてもおもしろいですね。

⇓こちらがフィボナッチタイルのワークシートです。記事の最後に有料ですがダウンロードできます。④のフィボナッチの行進ではまとめてダウンロードできます。

・・・でも

すぐにやってみたい？

裏技ですが、、、パソコンに画像を保存して、画用紙に印刷して
フィボナッチタイルを描いてもOKですよ（＾＾）

糸かけだとこんな感じです。１５cm×１５cmの板で作っています。
まずは最初の１に糸を描ける（写真は赤）

隣にもう一つの1をかける（写真はピンク）
そして、下にいき２をかける（写真はオレンジ）１辺が２だから２×２で４個のマス目があるのがわかりますか？

４個あるからいろんな方向にかけてみてくださいね。

１+２＝３
左に進んで３で糸をかけます。１辺が３ですから３×３で９個のマス目がありますね。

次に上に上がって５です。１辺が５なので５×５で２５個のマス目が中にあります。

最後は８．６４個のマス目が中にあります。

色を入れていくときは、マス目ひとつひとつに入れていきます。
この時の進み方も、糸かけと同じに１，１，２，３，５，８で進んでくださいね。

次は②としてφや黄金比のお話をします。